Tactics for Handling Confidence Intervals, Chi-Square, and Regression on Exam Day

Preparing for upper-level statistics—demands more than memorizing formulas. These tests challenge you to think critically, interpret data accurately, and apply statistical theory with confidence under strict time limits. From calculating confidence intervals and mastering regression models to understanding hypothesis testing and bootstrapping, success hinges on both your knowledge and exam strategy. If you're feeling overwhelmed, you’re not alone. Many students turn to resources like Statistics Exam Helper platforms and Online Exam Help services to sharpen their skills and get expert guidance. But even with help, knowing how to prepare makes all the difference. This comprehensive guide breaks down key statistical concepts and offers proven techniques for tackling advanced exam questions with clarity and speed. Whether you're aiming for top marks or just want to pass with confidence, these strategies will help you feel more in control, more prepared, and ultimately more successful. Let’s turn that exam stress into exam strength—starting now.
Core Concepts You Must Master

Advanced statistics exams are structured to test your application of core statistical ideas in real-world contexts. Here's how to approach the critical topics that appear repeatedly in such assessments.
Confidence Intervals
Confidence intervals form the bedrock of statistical inference, and understanding them thoroughly can make or break your performance on the exam.
1.1 Know When to Use t vs. z Intervals
Many students stumble on this distinction. Use a z-confidence interval when the population variance is known and the sample size is large. Use a t-confidence interval when the population variance is unknown and the sample size is small (typically n < 30). For instance, in the basketball example from your exam, you must compute both a t and z interval for the same data set.
Exam Tip: Always look at the conditions carefully. The question may give you σ² explicitly (use z), or just the sample standard deviation (use t).
1.2 Understand What Confidence Actually Means
A 95% confidence interval does not mean there is a 95% probability the parameter is in the interval. It means that if we repeated the experiment 100 times, approximately 95 of the calculated intervals would contain the true parameter. This subtlety is often tested in theoretical questions.
Exam Tip: Be prepared to explain this concept in words. A short paragraph may be all it takes to grab easy marks.
1.3 Calculate Sample Sizes for Desired Confidence Levels
Questions like “How many samples do I need for a 95% confidence interval with width 1?” are common. These test your ability to manipulate the margin of error formula. Know this well:
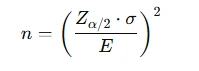
Exam Tip: Keep a cheat sheet of common Z-scores (e.g., Z₀.₀₂₅ = 1.96 for 95% CI).
Chi-Square Intervals
These often throw students off because they require right-tail critical values.
2.1 Understand When to Use a χ² Interval
You use a chi-square interval when estimating variance or standard deviation of a normally distributed population. For instance, when given a standard deviation from a sample of motel occupancy rates, you'll be asked to create a confidence interval for the true σ.
Formula:
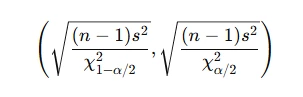
2.2 Practice Reading χ² Tables
Unlike z or t tables, chi-square tables give right-tail critical values. Make sure you use the correct degrees of freedom (n - 1), and the appropriate α values.
Exam Tip: Mark the chi-square table pages in your formula sheet so you can flip to them quickly.
Bootstrapping
Bootstrapping is a favorite on exams because it blends computation, interpretation, and statistical creativity.
3.1 Differentiate Between Parametric and Empirical Bootstrap
Parametric Bootstrap assumes you know the distribution (e.g., geometric(p)), and you resample based on estimated parameters.
Empirical Bootstrap resamples from the observed data directly, usually without assuming any underlying distribution.
Be clear on both techniques. Know the steps: resample → compute statistic → repeat → build interval.
3.2 Construct Confidence Intervals from Resampled Statistics
From a set of 200 bootstrapped sample medians or means, you will typically be asked to extract the middle 90% (i.e., the 5th and 195th values for a 90% CI).
Exam Tip: If sorting 200 values, look for the 10th and 190th values for a 90% CI. Use this general rule: for a (1 – α) CI out of N sorted values, trim (α/2 × N) from each end.
3.3 Interpret Bootstrapped Intervals
Always be prepared to comment on the nature of bootstrapped results. Does the interval suggest skewness? How does it compare with classical methods like t-intervals?
Strategic Preparation Tips for Exam Day
Understanding theory is only part of the challenge. The other half is managing your preparation and mental game. Here’s how to approach your study time and test-taking experience.
Practice With Real Exam Questions
1. Focus on Problem Types
Use old exams (like the Katie 2 practice exam) to identify recurring question types: confidence intervals, polling analysis, regression estimates. Group problems by type and practice solving them in batches.
Tip: For each type, develop a step-by-step “attack plan.” Example for CI:
- Check assumptions (normality, sample size).
- Choose correct distribution (t or z).
- Plug into formula.
- Interpret in context.
2. Time Yourself
Simulating test conditions is vital. Pick 4–5 practice questions, set a timer, and work without notes. This trains your brain to focus under pressure.
Tip: Use the last 10–15 minutes to check calculations, units, and logic.
Build Your Formula and Concept Bank
1. Create a One-Page Summary Sheet
Include:
- t, z, χ² critical values
- Margin of error formula
- CI formulas for mean, proportion, variance
- Regression equation: y = ax + b
Tip: Even if your exam is open-book, the act of preparing this sheet reinforces memory.
2. Memorize Intervals and Distributions
Not just formulas, but also their conditions of use:
- Use t-distribution if σ unknown.
- Use normal distribution for large samples or known σ.
- Use chi-square for variance estimation.
How to Handle Exam Hall Pressure
You’ve done the prep, now it’s game time. Handling statistics problems under pressure is a skill that can be learned.
Read Carefully and Identify the Test Type
The biggest source of lost marks is misunderstanding the question. Read every question twice. Is it asking for a confidence interval or a hypothesis test? Is it about mean, variance, or proportion?
Tip: Highlight or underline key terms like “95% CI,” “standard deviation,” or “MLE.”
Think Before You Calculate
It’s tempting to jump into plugging numbers into formulas, but that often leads to errors. First, ask:
- What distribution is involved?
- Do I know σ?
- What is the sample size?
- What is the parameter of interest (mean, proportion, median)?
Write a plan in bullet form before executing it.
Use Tables with Precision
In the provided exam, you’re expected to use t-tables, z-tables, and chi-square tables—all formatted differently. Familiarize yourself with:
- Left-tail vs. right-tail
- Interpolation (if needed)
- Degrees of freedom (n - 1 for t and χ²)
Tip: Practice retrieving values quickly. Bookmark table pages and learn approximate thresholds (e.g., z₀.₀₂₅ = 1.96).
Check and Interpret Your Answer
After you get a number, stop. Ask:
- Does this answer make sense?
- Does the interval capture the sample mean?
- Is it wider or narrower than expected? Why?
Always write an interpretation if asked. A complete answer includes both the interval and a sentence explaining what it means in real-world terms.
Final Thoughts
Success in advanced statistics exams hinges on conceptual understanding, methodical problem-solving, and calm execution under pressure. The topics covered—confidence intervals, bootstrapping, chi-square estimation, and regression—are not just academic abstractions; they are tools you’ll use in real-world data analysis. Preparing effectively means going beyond rote memorization: you must master when and how to use these tools, and why they matter. By understanding the structure of problems like those in the provided practice exam and by refining your study and exam strategies, you’ll not only improve your grade but also build confidence in one of the most essential skills in modern analytics: statistical reasoning.