How to Prepare for Financial Economics Exams Through Structured Topic Preparation

Dr. Lucas Henderson

Canada

Economics

Dr. Lucas Henderson is a Canada-based Financial Economics Exam Helper with over 10 years of experience supporting university students. He specializes in financial markets, econometrics, risk analysis, portfolio theory, and macroeconomic policy. Dr. Henderson delivers accurate, timely, and exam-focused solutions with clear explanations.

Hire Me to Take Your Economics Exam

Understanding the Core Structure of Financial Economics Exams

Before studying formulas, you must understand what examiners are actually testing. Financial Economics exams are not memory tests—they are application tests. The attached syllabus-style formula sheet reveals a clear structure: pricing logic → probabilistic modeling → risk-neutral valuation → hedging and interpretation.

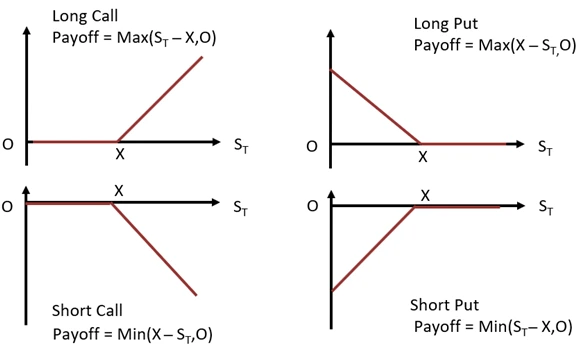
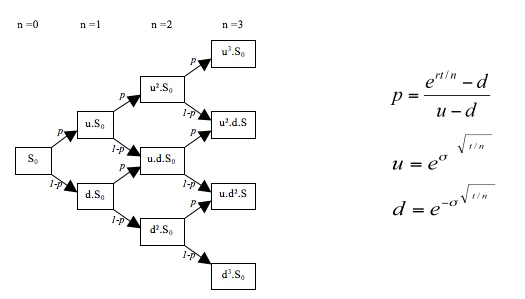
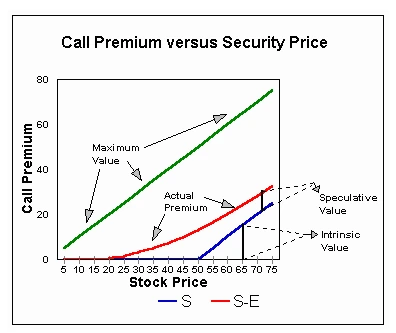
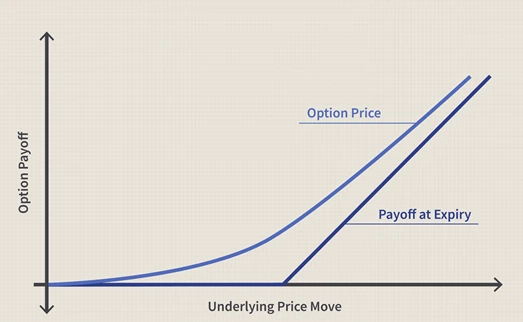
Forward Contracts, Put–Call Parity, and No-Arbitrage Logic

Almost every Financial Economics exam begins with foundational pricing logic. Forward contracts, prepaid forwards, and put–call parity are not isolated topics—they form the language of no-arbitrage reasoning.

When preparing, do not memorize formulas blindly. Instead, focus on:

1. Why forward prices adjust for interest rates and dividends
2. How put–call parity links calls, puts, and forwards
3. How arbitrage opportunities arise when inequalities are violated

Typical exam questions will:

1. Ask you to identify mispriced options
2. Construct arbitrage portfolios
3. Compare calls and puts across strikes or maturities

Preparation tip: Always rewrite pricing relations in plain language (“owning a call and cash replicates owning a stock plus a put”). This habit dramatically improves speed and confidence under pressure.

Binomial Trees and Risk-Neutral Pricing Framework

Binomial trees are not tested for complexity—they are tested for conceptual discipline. Students often lose marks by rushing calculations without understanding what each step represents.

Your preparation should emphasize:

1. Replicating portfolios (Δ and bond positions)
2. Risk-neutral probabilities and why they replace real probabilities
3. The difference between European and American exercise decisions

Exams frequently test:

1. One-step or two-step trees
2. Early exercise logic
3. Option valuation using backward induction

A common trap is forgetting to check early exercise at every node for American options. Build the habit of pausing at each node and asking: Is exercising better than holding?

Continuous-Time Models and Stock Price Dynamics

This section separates average students from top scorers. Topics like Brownian motion, geometric Brownian motion, and Itô’s lemma intimidate many candidates—but exams rarely test deep proofs. Instead, they test interpretation and application .

Focus your preparation on:

1. Recognizing arithmetic vs geometric Brownian motion
2. Understanding why stock prices are lognormal
3. Applying Itô’s lemma mechanically but correctly

Common exam tasks include:

1. Identifying the drift and volatility of transformed processes
2. Writing down SDEs for stock prices with dividends
3. Interpreting distributions and moments

Do not overthink stochastic calculus. Treat it like advanced differentiation with rules.

Mastering Pricing Models and Risk Management Topics

Once the probabilistic foundation is clear, exams move toward valuation models and risk measurement. This is where precision matters.

Black–Scholes Equation and Closed-Form Pricing

Black–Scholes is not about memorizing one formula—it is about understanding where each term comes from.

Your preparation should ensure you can:

• Identify d₁ and d₂ correctly
• Adjust formulas for dividends, currencies, and futures
• Switch between prepaid forward and spot-price versions

Exams commonly test:

• Calls vs puts using parity
• Interpretation of parameters (volatility, interest rates)
• Effects of changing σ, r, or T on option prices

Students lose marks by mixing real-world drift with risk-free rates. Drill the habit: pricing always uses the risk-neutral world.

Greeks, Hedging, and Risk Interpretation

Greeks transform pricing into risk management, which examiners love because it tests intuition.

You should prepare to:

• Interpret delta, gamma, and theta qualitatively
• Apply delta–gamma approximations
• Construct hedged portfolios

Exams often ask:

• Whether an option position benefits from volatility changes
• How to neutralize risk using underlying assets
• Approximate price changes using Taylor expansions

A powerful exam technique is sign analysis. Even if calculations are messy, identifying whether a Greek is positive or negative can earn partial or full conceptual marks.

Advanced Topics: Exotic Options, Simulations, and Interest Rates

Higher-level Financial Economics exams test whether you can extend core logic to unfamiliar settings.

Exotic Options and Payoff-Based Reasoning

Exotic options are rarely tested for full derivations. Instead, exams focus on payoff logic and parity relationships.

Your preparation should emphasize:

1. Understanding path-dependence (Asian options)
2. Knock-in vs knock-out logic for barrier options
3. Using parity instead of full pricing for compound options

When facing exotic options in exams:

1. Draw payoff diagrams mentally
2. Reduce the problem to familiar European options whenever possible
3. Use given parity relationships confidently

Monte Carlo Simulation and Estimation Questions

Simulation questions test process understanding, not programming.

Prepare by mastering:

1. How lognormal stock prices are simulated
2. Why averaging payoffs and discounting works
3. Variance reduction intuition (antithetic variates, stratification)

Exams often ask:

1. Steps in a Monte Carlo pricing algorithm
2. How estimation error behaves
3. Why simulation converges slowly

A clean, structured explanation often scores more than formulas alone.

Interest Rate Trees and Short-Rate Models

Interest rate topics are conceptually heavy but procedurally repetitive.

Focus preparation on:

1. Zero-coupon bond pricing
2. Forward rates and caplet payoffs
3. Understanding Vasicek, CIR, and tree-based models at a high level

Examiners usually test:

1. Correct setup of trees
2. Interpretation of mean reversion
3. Risk-neutral valuation logic

Do not attempt to memorize every model. Instead, understand the common structure behind them.

Exam Hall Strategy for Financial Economics Exams

This section alone can improve scores by 20–30%.

Reading and Planning Before Solving

Spend the first 5–10 minutes:

• Identifying question types (pricing, proof, interpretation)
• Marking formula-heavy vs explanation-heavy questions
• Choosing an optimal order

Never start with the hardest question unless required.

Structuring Answers for Maximum Marks

Markers look for logic, not just numbers.

Always:

• Write the relevant formula first
• Define variables clearly
• Show intermediate steps

Even if the final answer is wrong, structure earns partial credit.

Managing Time and Stress Effectively

If stuck:

• Write known relationships
• State assumptions clearly
• Move on and return later

Financial Economics rewards calm reasoning, not speed alone.

Final Thoughts: Preparing Smart Beats Studying Hard

Financial Economics exams are predictable once you understand their structure. The attached syllabus-style formula coverage shows that success depends on:

1. Strong foundations in no-arbitrage logic
2. Comfort with probabilistic modeling
3. Clear interpretation of pricing and risk measures
4. Strategic execution in the exam hall

With disciplined topic-wise preparation and smart exam techniques, even the most complex Financial Economics papers become manageable—and scoring well becomes realistic rather than intimidating.